土豆不吃鱼

• 蒙特卡洛法计算圆周率误差分析
  • 随机误差
  • 分析概率分布
  • 实验环节
  • 总结
  • 题外话

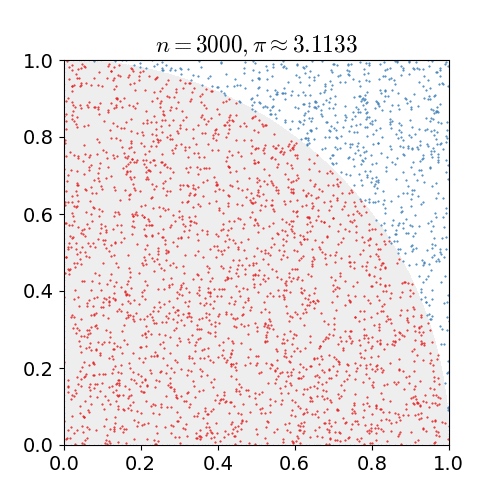
早期有一篇公众号文章介绍了蒙特卡洛法计算圆周率，也是中学课本的经典例子，投掷大头针的方法来计算圆周率。用计算机模拟的本质就是从边长为2的正方形中均匀采样，如果样本点落中单位圆内则计数器加1，最终用落在单位圆内的点除以总的样本点，近似等于圆的面积除以正方形面积。

$\frac{圆内点个数}{总样本点} = \frac{圆的面积}{正方形面积}$

$\frac{m}{N} = \frac{\pi}{4}$

由于是单位圆，所以圆的面积在数值上就等于圆周率，只需要统计出总样本点和圆内样本点即可。那么问题来了，蒙特卡洛法的特点是结果具有随机性，那么我们最终计算的结果精度是多少呢？误差怎么计算呢？如果想要得到小数点后5位精度的结果，需要多少次的模拟试验呢？

之前的文章我们无法回答这个问题，我们只能定性的知道，采样点越多，其结果应该越准确，但采样点的个数与精度到底什么关系，我们并不知道，本文就是来回答这些问题。

随机误差

模拟是指把某一现实的或抽象的系统的某种特征或部分状态，用另一系统（称为模拟模型）来代替或模拟。 为了解决某问题，把它变成一个概率模型的求解问题，然后产生符合模型的大量随机数，对产生的随机数进行分析从而求解问题，这种方法叫做随机模拟方法，又称为蒙特卡洛(Monte Carlo)方法。

随机模拟方法会引入所谓随机模拟误差：上例中对于圆周率的估计，实际是随机的，如果再次独立重复投个点，得到的和上一次结果会有不同。 这是随机模拟方法的特点，即结果具有随机性。因为结果的随机性导致的误差叫做随机模拟误差。

分析概率分布

前面的文章讲完了常用的概率分布和采样的一些基础了，现在可以利用前面的内容来分析服从的概率分布了。首先来看总的采样$N$次中，其中落在圆内的次数$m$应该服从什么分布？应该是伯努利分布（或者二项分布），这是因为每次采样都可以看成是独立重复试验，事件就是样本点落在圆内,那么事件发生的概率就是$\pi / 4$，也就是说$m \sim B(n, \frac{\pi}{4})$

接下来看估计值$\hat \pi$服从什么分布？根据中心极限定理，估计值$\hat \pi$服从正态分布，$\hat \pi \sim N(\mu, \sigma)$正态分布有两个参数$\mu, \sigma$，其中$\mu$直接给出就是$\pi$，做物理实验时，为什么要多次测量求平均值的道理，就是为了消除随机误差。接下来计算方差：

$\sigma^2 = D(\hat \pi) = D(\frac{4m}{N}) = \frac{4^2}{N^2} D(m)$

由于$m \sim B(n, \frac{\pi}{4})$，$D(m) = N\frac{\pi}{4}(1-\frac{\pi}{4})$.
于是方差就可以得到：

$\sigma^2 = \frac{\pi(4-\pi)}{N}$

我们知道了$\hat \pi \sim N(\mu, \sigma)$，根据正态分布的$3\sigma$原则，会有95%的点都落在$(\mu-2\sigma,\mu+2\sigma)$，99.7%的点落在$(\mu-3\sigma,\mu+3\sigma)$。我们发现$\sigma = \sqrt \frac{\pi(4-\pi)}{N}$,通过增加试验次数可以缩小方差，也就是将误差控制在一定范围内，误差每减小$1/10$，需要增加100倍的实验样本。

实验环节

从实验结果可以看出，实验次数每增加100倍，95%误差界缩小为原来的$1/10$；根据实验次数与随机模拟误差两列，可以看出实验次数与精度的关系，需要得到两位有效数字，样本数不得低于1万次，样本数据在10万次，可以较好地保证两位有效数字。

备注：至于实现代码应该不需要吧，如果有不理解的可以在后台留言，愿意帮助你完成代码实现。

总结

本文在蒙特卡洛法的基础上，进一步介绍了误差分析，回答了文章开头提到的问题，最终也找到样本点个数与误差之间的关系，总结随机模拟方法有如下特点：

1. 应用面广，适应性强。只要问题能够清楚地描述出来， 就可以编写模拟程序产生大量数据， 通过分析模拟数据解决问题。
2. 算法简单, 容易改变条件, 但计算量大
3. 结果具有随机性，精度较低(一般为$O(\frac{1}{\sqrt N})$级)
4. 模拟结果的收敛服从概率论规律
5. 对维数增加不敏感。在计算定积分时,如果使用传统数值算法，维数增加会造成计算时间指数增加， 但是如果使用随机模拟方法计算， 则维数增加常常仅仅使计算时间随维数增加而线性地增加

题外话

很抱歉最近挺长时间没有更新文章，最开始我先阳了，休息了一周时间，刚开始上班两天，老婆孩子也先后阳了，于是只能休假回家照顾，前后十多天时间没有更新，目前都已经恢复了正常。统计学的内容还会继续更新，希望与各位读者朋友多交流。