计算机如何产生“随机数”

计算机很容易产生随机数，很多编程语言提供了非常便捷的接口，获取各种条件的随机数。这篇文章主要介绍计算机是如何得到这些随机数的。理解本文需要一点点数列知识。

目标

本文提到的随机数是均匀分布的随机数。获取一定范围内的随机数，意味着在这个范围内，每个数被抽样的概率是相等的。比如我们产生0-9范围内的随机整数，连续取10个数，每个数的概率要尽量均衡，这样的随机数的“随机性”是比较好的。当然只取10个数肯定太少了，我们可以生成大量(上亿个)数来统计概率分布，越是均匀意味着随机性越好。

明确了这个目标以后，接下来思考计算机如何产生随机数？由于计算机是确定系统，底层的逻辑电路接受确定的输入，输出也是确定的。意味要得到现实世界的真随机数是做不到的，那就只能生成一些“伪随机数”，保证概率分布是均衡的，这样的伪随机数就能起到“以假乱真”的效果了。

随机数的产生

设随机变量 $X$ 有分布函数 $F(X)$ , $X_i, i=1,2,3...$ 是独立同分布，则 $X_i$ 的一次观测的数值 $x_i$ 叫做分布的随机数序列，简称随机数。随机数是统计中一个重要的计算工具“随机模拟”的基本构成元素。

我们可以用物理方法得到一组真实的随机数，比如反复抛掷硬币、骰子、正二十面体骰子，抽签、摇号，等等。这些方法得到的随机数质量好，但是数量不能满足随机模拟的需要。另一种办法是预先生成大量的真实随机数存储起来，进行随机模拟时读取存储的随机数。这种方法的速度较低，已经被取代了。

计算机中伪随机数序列是迭代生成的即 $x_n = g(x_{n-1}, x_{n-2}, \cdots, x_{n-p})$ 是一个非线性函数。如何找到这样的 $g$ ，使得产生的序列呈现出随机性?首先要使结果有随机性。比如，把一个大的整数平方后取中间的位数，然后递推进行，叫做平方取中法。这种方法均匀性差而且很快变成零，所以已经不再使用。还可以把序列的前两项相乘然后取中间的数字，这种方法也有类似缺点.

现在常用的均匀分布随机数发生器有线性同余法、反馈位寄存器法以及随机数发生器的组合。均匀分布随机数发生器生成的是 $0,1,2,\cdots,M$ 上离散取值的离散均匀分布，然后除以 $M$ 或变成 $[0,1]$ 内的值当作连续型均匀分布随机数，实际上是只取了有限个值。因为取值个数有限，根据算法 $x_n = g(x_{n-1}, x_{n-2}, \cdots, x_{n-p})$ 可知序列一定在某个时间发生重复，使得序列发生重复的间隔叫做随机数发生器的周期。 好的随机数发生器可以保证很大而且周期很长.

线性同余发生器

线性同余随机数发生器是利用求余运算的随机数发生器。其递推公式为

x_n = (ax_{n-1} + c )\quad (mod \quad M) , n=1,2,3,...

这里等式右边的 $(ax_{n-1} + c )\quad (mod \quad M)$ 表示 $a x_{n-1} + c$ 除以 $M$ 的余数.其中 $a$ 是正整数， $c$ 为非负整数，取一个非负数初值 $x_0$ 就可以递推，得到非负数序列。最后令 $R_n = x_n / M$ 把 $R_n$ 做为 $[0,1)$ 的均匀分布随机数序列。这样的算法的基本思想是因为很大的整数前面的位数是重要的有效位数而后面若干位有一定随机性。如果取 $c=0$ 线性同余发生器称为乘同余发生器, 如果取 $c>0$ 线性同余发生器称为混合同余发生器。

下面来看几个线性同余发生器

考虑线性同余发生器 $x_n = 7x_{n-1} + 7 \quad mod \quad 10$ ,取初值 $x_0 = 1$ ,数列为 $(7,6,9,0,7,6,9,0,7,...)$ 周期为 $T=4< M = 10$ .
考虑线性同余发生器 $x_n = 5x_{n-1} + 1 \quad mod \quad 10$ ，取初值 $x_0 = 1$ ，数列为 $(1,6,1,6,...)$ ，显然周期为 $T=2$
考虑线性同余发生器 $x_n = 7x_{n-1} + 7 \quad mod \quad 8$ ,取初值 $x_0 = 1$ ,数列为 $(1,6,7,4,5,2,3,0,1,6,7...)$ 周期为 $T=8 = M$ 达到最大周期。

从上面的例子可以发现不同的 $M,a,c$ 选取的方法不同得到不同的周期，适当的取值能产生随机数序列和真正的 $U(0,1)$ 随机数表现相近。好的随机数意味着 $M,a,c$ 的取值，使得生成的序列越多周期越大

案例

接下来看一个效果比较好的混合同余发生器，是Kobayashi提出了的满周期 $2^{31}$ 的混合同余发生器

x_n = (314159269 x_{n-1} + 453806245) \quad( mod \quad 2^{31})

def random(num=1, seed=0):
    ans = []
    x = seed
    for _ in range(num):
        x = (314159269 * x + 453806245) % 2 ** 31
        ans.append(x / 2 ** 31)
    return ans
    
>>> random(5)
[0.2113200002349913, 0.010224699042737484, 0.1883314079605043, 0.66593280993402, 0.9833076749928296]

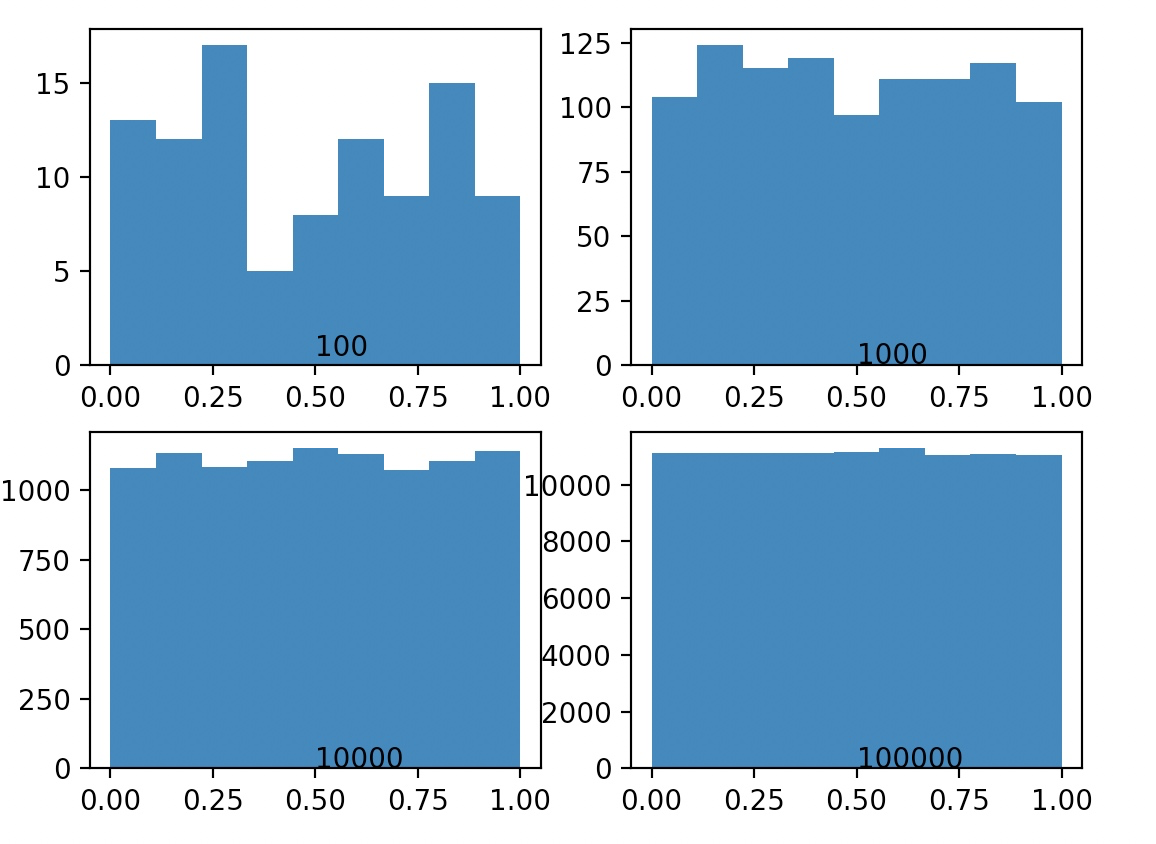
接下来我们随机生成100，1千，1万，10万个点，然后分别统计他们的分布，如下图可以看到，产生1万个随机数分布已经相对均匀了，说明生成的随机数的质量挺高的。seed成为随机数的种子，相同的种子生成的“随机数”是一样的。

总结

本文介绍了生成伪随机的一种方法，线性同余发生器。通过简单的数列迭代就能生成大量的随机数，通过这种方式就能得到在0-1区间内的均匀分布，其实很多分布可以根据均匀分布变换，从而得到更多的概率分布，后面的文章会继续介绍生成已知概率分布的数，比如生成100个点，服从标准正态分布的，这就是采样了。

参考

李东风.《统计计算》

土豆不吃鱼