本篇文章整理常用的一些概率分布,这些经典的概率分布是实际生活中非常有用。之后的文章都会用到这些基础的概率分布。

离散型分布

离散型随机变量：随机变量可能取值能够一一列出来有限个或可列无限个。
假设离散型随机变量$X$,可能取值为$x_1, x_2, \cdots, x_n,\cdots$，对应取值的概率为:

$p_k = P \{X=x_k\}, (k=1,2,\cdots)$

成为X的分布列或者概率分布，一般都用表格来表示。离散型随机变量具有两个性质：

1. 非负性 $p_k \ge 0$
2. \sum_\limits{i=1} ^\infty p_k = 1

单点分布

随机变量$X$以概率1取常数c，即

$P\{X=c\} = 1$

两点分布

随机变量$X$的概率分布为：

$P\{X=1\} = p, P\{X=0\} =1- p$

则称$X$服从两点分布或者0-1分布，两点分布是描述只有两种可能结果的随机现象的概率模型，如是或否，抛硬币的正面或者反面等。

二项分布

随机变量$X$的取值为$0，1，2，3,...,n$共$n+1$个，且概率分布为：

$P\{X=k\} = C_n^kp^k(1-p)^{n-k}$

记$X \sim B(n, p)$，二项分布也成为伯努利分布。

二项分布的使用场景典型的是抓红黑球的实验。已知盒子里有20个大小材质相同的球，其中红球12个，黑球8个，又放回的从盒子中连续抽取5个球，求出红球的概率分布。类似这样的问题称为独立重复实验，抓到红球的概率为$\frac 3 5$，于是随机变量$X$服从$B(5, 0.6)$的二项分布。

泊松分布

假设随机变量$X$的取值为$0，1，2，3,...$其概率分布为：

$P\{X=k\} = \frac{\lambda ^k}{k!}\mathrm e^{-\lambda}$

其中$\lambda >0$则称$X$服从参数为$\lambda$的泊松分布，记为$X\sim P(\lambda)$

泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。如某一服务设施在一定时间内受到的服务请求的次数，电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数、放射性原子核的衰变数、激光的光子数分布等等。

几何分布

随机变量$X$表示在伯努利试验中，得到一次成功所需要的试验次数，如果每次试验的成功概率是$p$，那么$k$次试验中，第$k$次才得到成功的概率是

$P\{X=k\} = (1-p)^{k-1} p$

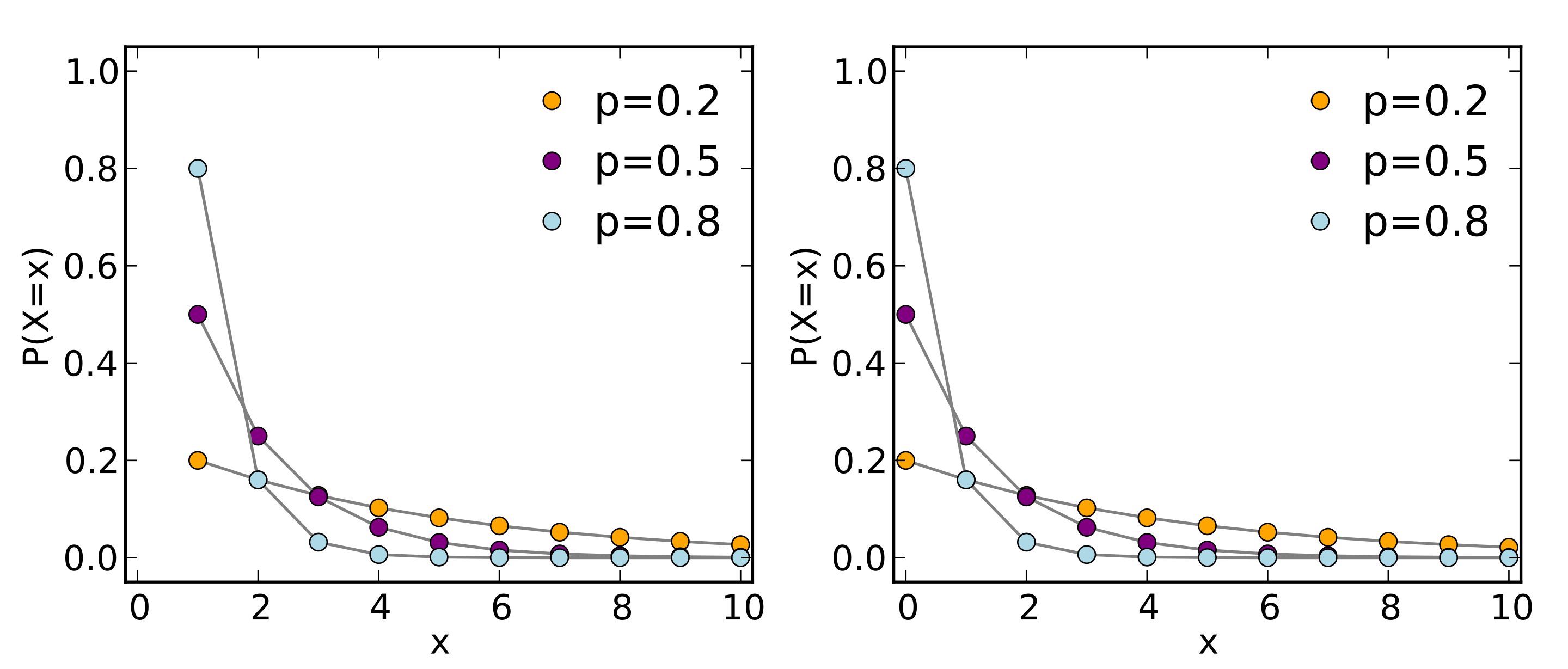
其中k的取值不同，含义略有差异，下图中k从1开始取值，表示第$k$次才得到成功的概率，k从0开始取值，表示前面k次失败的概率，也就是$k+1$成功，两种都是几何分布。

连续型分布

连续性随机变量我们通常用概率密度函数来表示，如果随机变量$X$存在一个非负的可积函数$p(x)$，对人意的实数$a,b(a<b)$均有

$P\{a<x\le b\} = \int_a^b f(x)\mathrm dx$

成立，称$X$为连续性随机变量，$p(x)$为$X$的概率密度函数，简称概率密度。

均匀分布

假设随机变量$X$的取值在区间$(a,b)$内，且具有概率密度

$p(x) = \frac{1}{b-a} ,a \lt x \lt b$

均匀分布的特点是对于一定长度的区间$I \subseteq (a,b)$，无论在$(a,b)$的什么位置，只要长度不变，有相同的概率

$P\{X\in I\} = \int_I \frac{\mathrm dx}{b-a} = \frac{||I||}{b-a}$

正态分布

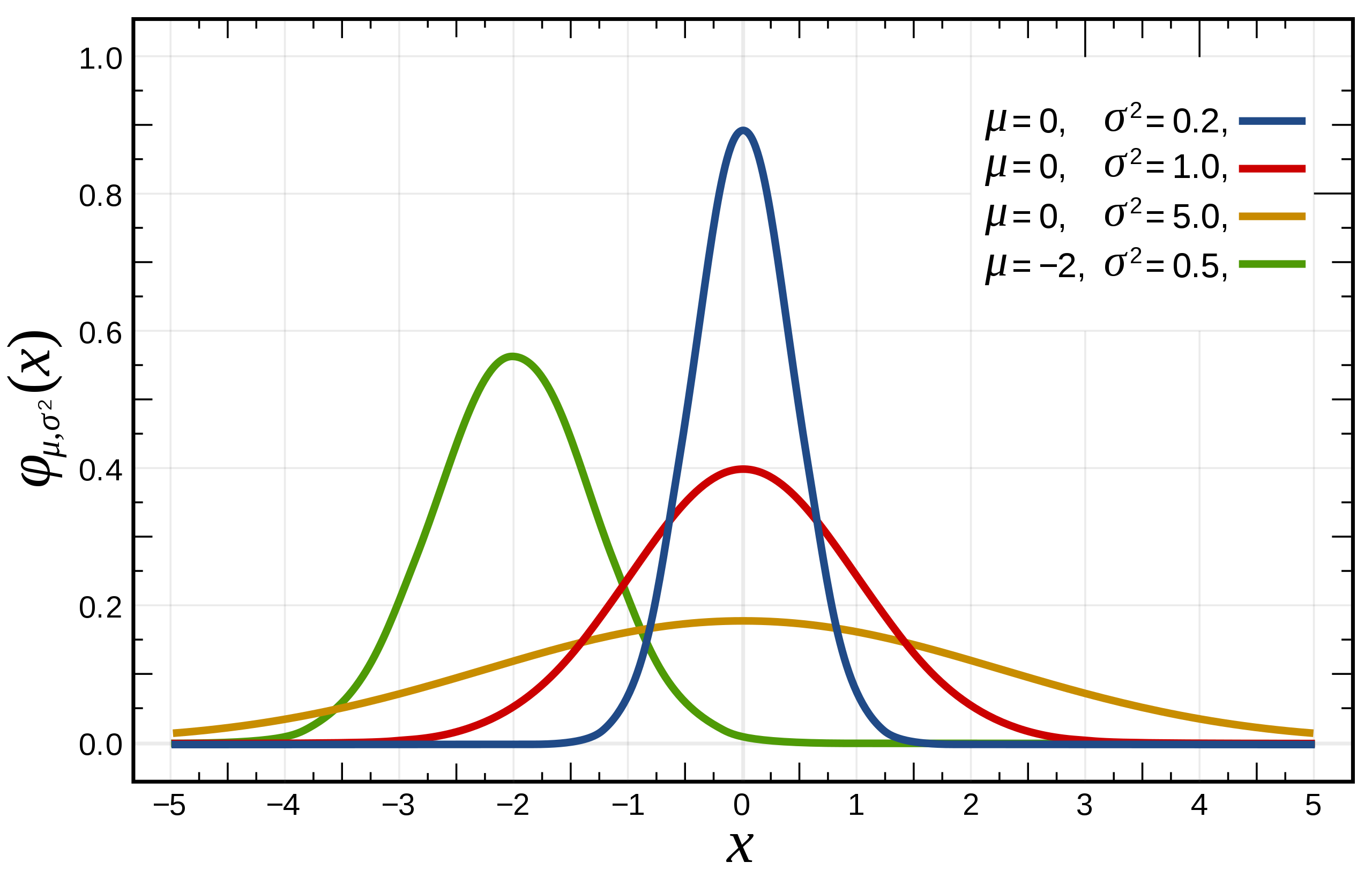
随机变量$X$的概率密度函数为

$p(x) = \frac{1}{\sigma \sqrt{2\pi}} \mathrm e^{-\frac{(x-\mu)^2}{2\sigma^2}}, -\infty \lt x \lt \infty$

其中 $\sigma \gt 0,\mu$ 为常数，则称$X$服从参数$\sigma,\mu^2$的正态分布或者高斯分布。记为$X\sim N(\mu, \sigma ^2)$

指数分布

随机变量$X$取值于$[0,+\infty)$，且以

$p(x) = \lambda \mathrm e^{-\lambda x},x>0$

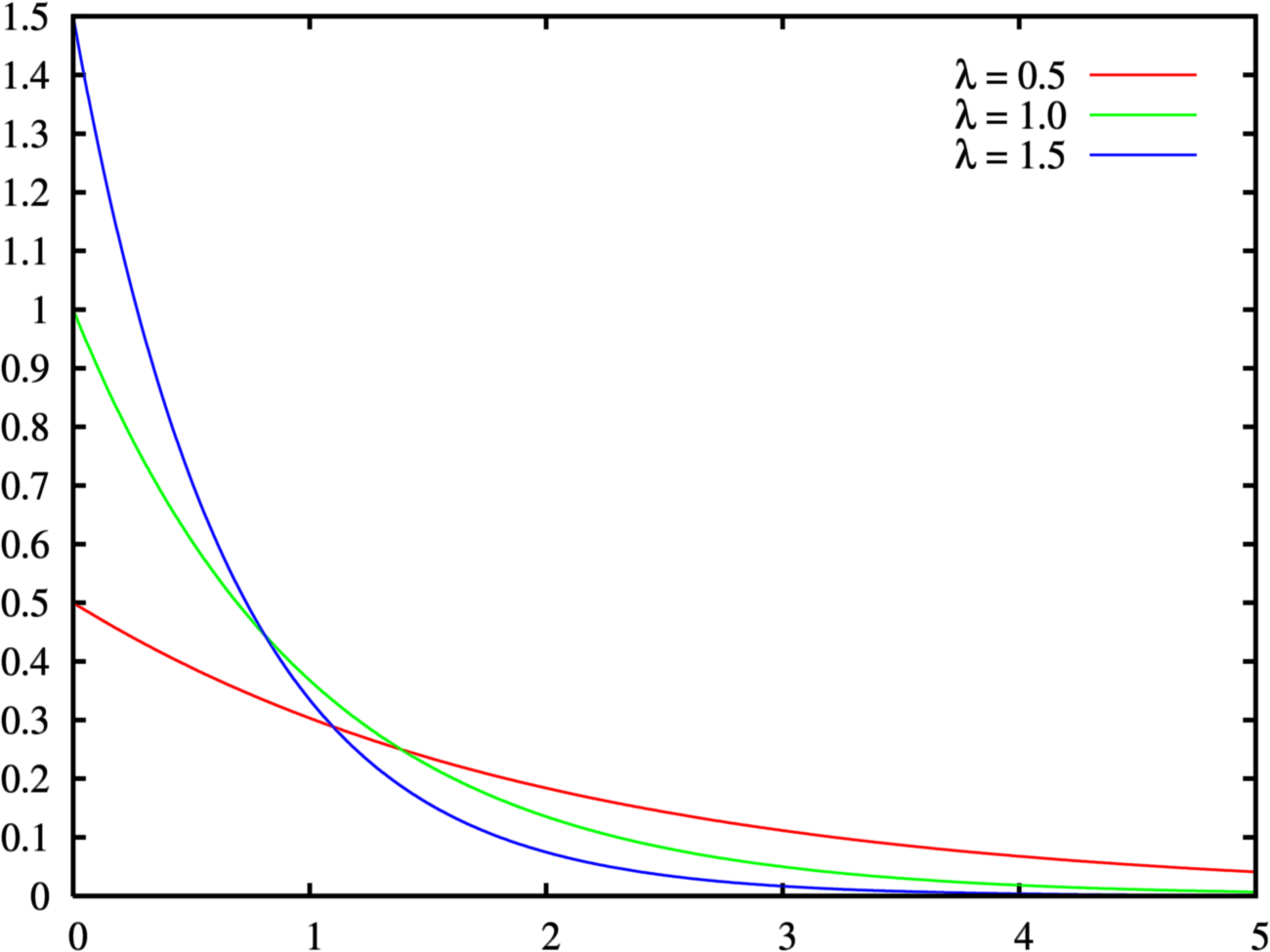
指数分布可以用来表示独立随机事件发生的时间间隔，比如旅客进入机场的时间间隔、电话打进客服中心的时间间隔、中文维基百科新条目出现的时间间隔、机器的寿命等。

总结

本文简单的介绍了一些常用的概率分布，包括离散型和连续型，仅仅只是列举了概率分布，没有过多的介绍不同分布之间的内在关联，后续的文章还会继续介绍。